조화 평균

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 가중 조화 평균
3. 성질
4. 다른 평균과의 관계
5. 응용
6. 통계
7. 베타 분포, 로그정규분포, 파레토 분포
참조

1. 개요

조화 평균은 양의 실수들의 평균을 구하는 방법 중 하나로, 역수들의 산술 평균의 역수로 정의된다. 가중 조화 평균도 존재하며, 모든 데이터가 같지 않은 경우 조화 평균은 산술 평균, 기하 평균과 비교했을 때 가장 작은 값을 갖는다. 조화 평균은 물리학, 금융, 기하학, 정보 과학 등 다양한 분야에서 활용되며, 특히 비율이나 비를 포함하는 상황에서 유용하게 사용된다. 통계적으로는 표본의 성질을 추정하는 데 사용되며, 베타 분포, 로그정규분포, 파레토 분포 등 특정 분포의 조화 평균도 정의된다.

더 읽어볼만한 페이지

기술통계학 - 멱평균
멱평균은 양의 실수에 대해 정의되는 평균의 종류로, 지수 p를 사용하여 계산되며, p 값에 따라 조화 평균, 기하 평균, 산술 평균 등 다양한 특수한 경우를 나타낸다.
기술통계학 - 기하중앙값
기하 중앙값은 m개의 점 집합에서 각 점까지의 유클리드 거리의 합을 최소화하는 점이며, 1차원 공간에서 중앙값과 같고 유클리드 닮음 변환에 대해 공변성을 갖는다.
수학 - 귀류법
귀류법은 증명하려는 명제의 결론을 부정하여 모순을 이끌어냄으로써 원래 명제가 참임을 증명하는 방법이다.
수학 - 멱평균
멱평균은 양의 실수에 대해 정의되는 평균의 종류로, 지수 p를 사용하여 계산되며, p 값에 따라 조화 평균, 기하 평균, 산술 평균 등 다양한 특수한 경우를 나타낸다.
평균 - 제곱평균제곱근
제곱평균제곱근(RMS)은 값들의 크기를 나타내는 통계량으로, 이산 데이터의 경우 각 값의 제곱의 평균의 제곱근, 연속 함수의 경우 함수 제곱의 적분 평균의 제곱근으로 정의되며, 전기공학, 물리학 등 다양한 분야에서 활용되고 표준편차와 밀접한 관련이 있다.
평균 - 표본 평균
표본 평균은 모집단의 모평균을 추정하기 위해 표본에서 추출된 값들의 산술 평균을 구한 것으로, 표본 내 변수 값들의 합을 값의 개수로 나눈 값이며, 불편성을 가지고 확률 변수이며 자체적인 분포를 갖는다.

조화 평균
기본 정보
학문 분야	수학
하위 분야	실해석학, 통계학
관련 개념	평균, 산술 평균, 기하 평균, 제곱 평균, 일반화 평균
정의
정의	주어진 양수 값들의 역수들의 산술 평균의 역수
수식	N개의 양수 값 x₁, x₂, ..., xₙ에 대하여 조화 평균 H는 다음과 같이 정의됨: H = N / (∑(1/xᵢ)) 여기서 ∑는 i=1부터 N까지의 합을 나타냄.
특징	모든 변수가 동일한 경우 산술 평균과 같음. 극단적인 값에 민감하게 반응함. 주로 비율이나 속도와 관련된 데이터 분석에 사용됨.
활용
활용 분야	물리학: 여러 저항의 병렬 연결 시 총 저항 계산 경제학: 주가 지수 계산 컴퓨터 과학: 알고리즘 성능 평가 스포츠: 타율 계산 공학: 유체 역학, 열전달 등의 문제 해결
예시
예시	2와 8의 조화 평균은 3.2임. (2 + 8) / 2 = 5 (산술 평균), 2 * 8 = 16, √16 = 4 (기하 평균), 2 / (1/2 + 1/8) = 3.2 (조화 평균)
추가 설명	조화 평균은 데이터 집합의 중심 경향을 나타내는 방법 중 하나이며, 특히 비율이나 속도와 같은 데이터에 적합함. 극단적인 값이 존재할 경우 산술 평균보다 더 안정적인 결과를 제공할 수 있음.
참고
관련 항목	산술 평균 기하 평균 제곱 평균 일반화 평균 평균

2. 정의

양의 실수 $x_1, x_2, \ldots, x_n$ 의 조화 평균 ''H''는 다음과 같이 정의된다.^[4]

: $H(x_1, x_2, \ldots, x_n) = \frac{n}{\displaystyle \frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}} = \frac{n}{\displaystyle \sum_{i=1}^n \frac{1}{x_i}}.$

이는 역수들의 산술 평균의 역수와 같으며, 그 반대도 마찬가지이다.

: $\begin{align}H(x_1, x_2, \ldots, x_n) &= \frac{1}{\displaystyle A\left(\frac{1}{x_1}, \frac{1}{x_2}, \ldots \frac{1}{x_n}\right)}, \\A(x_1, x_2, \ldots, x_n) &= \frac{1}{\displaystyle H\left(\frac{1}{x_1}, \frac{1}{x_2}, \ldots \frac{1}{x_n}\right)},\end{align}$

여기서 산술 평균은 $A(x_1, x_2, \ldots, x_n) = \tfrac{1}{n} \sum_{i=1}^n x_i.$ 이다.

두 수가 주어졌을 때, 두 수의 조화 평균은 다음 식으로 간단히 정리된다.

: $H = \frac{2 a_1 a_2}{a_1 + a_2}.$

이때, 산술 평균 $A = \frac{a_1 + a_2}{2}$ 과 기하 평균 $G = \sqrt{a_1 \cdot a_2}$ 에 대해 조화 평균은 $H = \frac{G^2}{A}$ 의 관계식이 성립한다.

조화 평균은 슈어-오목 함수이며, 그 인수들의 최솟값보다 크거나 같다. 따라서, 적어도 하나의 값을 변경하지 않고 일부 값을 더 크게 변경하여 조화 평균을 임의로 크게 만들 수 없다. 조화 평균은 또한 양의 인수에 대해 오목 함수이다.

2. 1. 가중 조화 평균

가중치 함수(가중치)

w_1

, ...,

w_n

가 데이터 집합

x_1

, ...,

x_n

에 할당되는 경우, '''가중 조화 평균'''은 다음과 같이 정의된다.^[9]

:

H = \frac{\sum\limits_{i=1}^n w_i}{\sum\limits_{i=1}^n \frac{w_i}{x_i}}= \left( \frac{\sum\limits_{i=1}^n w_i x_i^{-1}}{\sum\limits_{i=1}^n w_i} \right)^{-1}.

가중치가 모두 같은 특수한 경우를 비가중 조화 평균이라고 할 수 있다. 모든 가중치가 같은 임의의 집합에 대한 가중 조화 평균은 조화 평균과 같다.

3. 성질

조화 평균은 슈어-오목 함수이며, 그 인수들의 최솟값보다 크거나 같다.^[4] 양의 인수에 대해, $\min(x_1 \ldots x_n) \le H(x_1 \ldots x_n) \le n \min(x_1 \ldots x_n)$ 이다. 조화 평균은 또한 양의 인수에 대해 오목 함수이다.

모든 ''양의'' 데이터 집합에서 ''적어도 하나의 서로 다른 값의 쌍이 존재하는 경우'', 조화 평균은 항상 피타고라스 평균(산술 평균, 기하 평균, 조화 평균) 중 가장 작은 값이며,^[5] 산술 평균은 항상 가장 큰 값이고 기하 평균은 항상 그 중간에 있다.

이는 멱평균의 특수한 경우 ''M''₋₁이다.

$H\left(x_1, x_2, \ldots, x_n\right) = M_{-1}\left(x_1, x_2, \ldots, x_n\right) = \frac{n}{x_1^{-1} + x_2^{-1} + \cdots + x_n^{-1}}$

숫자 목록의 조화 평균은 목록의 가장 작은 요소에 강하게 치우치므로, (산술 평균과 비교하여) 큰 이상값의 영향을 완화하고 작은 이상값의 영향을 악화시키는 경향이 있다.

조화 평균은 다른 피타고라스 평균과 다음과 같은 관계를 가진다.

$H\left(x_1, \ldots, x_n\right) =\frac{\left(G\left(x_1, \ldots, x_n\right)\right)^n}{A\left(x_2 x_3 \cdots x_n, x_1 x_3 \cdots x_n, \ldots, x_1 x_2 \cdots x_{n-1}\right)} =\frac{\left(G\left(x_1, \ldots, x_n\right)\right)^n}{A\left(\frac{1}{x_1} {\prod\limits_{i=1}^n x_i},\frac{1}{x_2} {\prod\limits_{i=1}^n x_i},\ldots,\frac{1}{x_n} {\prod\limits_{i=1}^n x_i}\right)}.$

서로 다른 숫자 집합에 평균 보존 확산이 적용되는 경우 — 즉, 집합의 두 개 이상의 요소가 서로 "분산"되는 반면 산술 평균은 변경되지 않은 경우 — 조화 평균은 항상 감소한다.^[7]

두 수 $x_1$ 와 $x_2$ 의 특수한 경우에, 조화 평균은 다음과 같이 쓸 수 있다.^[4]

: $H = \frac{2x_1 x_2}{x_1 + x_2} \qquad$ 또는 $\qquad \frac{1}{H} = \frac{(1/x_1) + (1/x_2)}{2}.$

이 특수한 경우에, 조화 평균은 산술 평균 $A = \frac{x_1 + x_2}{2}$ 과 기하 평균 $G = \sqrt{x_1 x_2}$ 와 다음과 같은 관계가 있다.^[4]

: $H = \frac{G^2}{A} = G\left(\frac{G}{A}\right).$

산술평균과 기하평균의 부등식에 의해 $\tfrac{G}{A} \le 1$ 이므로, ''n'' = 2인 경우 ''H'' ≤ ''G''임을 보여준다. 또한 $G = \sqrt{AH}$ 이므로, 두 수의 기하 평균은 그 산술 평균과 조화 평균의 기하 평균과 같다.

세 개의 수 $x_1$ , $x_2$ 및 $x_3$ 에 대한 조화 평균은 다음과 같이 쓸 수 있다.^[4]

: $H = \frac{3 x_1 x_2 x_3}{x_1 x_2 + x_1 x_3 + x_2 x_3}.$

세 개의 양수 ''H'', ''G'', 및 ''A''가 세 개의 양수의 조화 평균, 기하 평균 및 산술 평균일 필요충분조건^[8]은 다음 부등식이 성립하는 것이다.

: $\frac{A^3}{G^3} + \frac{G^3}{H^3} + 1 \le \frac3{4} \left(1 + \frac{A}{H}\right)^2.$

데이터에 0이 하나 이상 있을 경우, 조화 평균은 0으로 극한을 취한다. 조화 평균의 값은 데이터 집합의 최솟값에 가까워지는 경향이 있다. 어떤 데이터 집합이 다른 데이터 집합을 mean-preserving spread한 것이라면 조화 평균은 원래 집합의 조화 평균보다 작아진다.^[38]

4. 다른 평균과의 관계

조화 평균은 멱평균의 특수한 경우 ''M''₋₁이다. 조화 평균, 산술 평균, 기하 평균 사이에는 다음과 같은 관계가 성립한다.

모든 ''양의'' 데이터 집합에서 ''적어도 하나의 서로 다른 값의 쌍이 존재하는 경우'', 조화 평균은 항상 세 가지 피타고라스 평균 중 가장 작은 값이며,^[5] 산술 평균은 항상 가장 큰 값이고 기하 평균은 항상 그 중간에 있다. (비어 있지 않은 데이터 집합의 모든 값이 같다면 세 평균은 항상 같다.)

이는 멱평균의 특수한 경우 ''M''₋₁이다:

$H\left(x_1, x_2, \ldots, x_n\right) = M_{-1}\left(x_1, x_2, \ldots, x_n\right) = \frac{n}{x_1^{-1} + x_2^{-1} + \cdots + x_n^{-1}}$

두 수 a, b의 세 가지 피타고라스 평균의 기하학적 구성. H는 조화 평균을 나타내는 보라색 선이다. A, G는 각각 산술 평균, 기하 평균을 나타낸다. 또한, Q는 제곱 평균 제곱근을 나타낸다.

양의 실수 집합에 대해, 조화 평균을 H, 산술 평균을 A, 기하 평균을 G라고 하면, 세 평균 사이에는 H ≤ G ≤ A의 관계가 성립한다. 평균을 취하는 수의 값이 모두 같을 때, 그리고 그 때에만 세 평균은 같아진다.

두 수

x_1

와

x_2

의 특수한 경우에, 조화 평균은 다음과 같이 쓸 수 있다.^[4]

:

H = \frac{2x_1 x_2}{x_1 + x_2} \qquad

또는

\qquad \frac{1}{H} = \frac{(1/x_1) + (1/x_2)}{2}.

이 특수한 경우에, 조화 평균은 산술 평균

A = \frac{x_1 + x_2}{2}

과 기하 평균

G = \sqrt{x_1 x_2}

와 다음과 같은 관계가 있다.^[4]

:

H = \frac{G^2}{A} = G\left(\frac{G}{A}\right).

산술평균과 기하평균의 부등식에 의해

\tfrac{G}{A} \le 1

이므로, ''n'' = 2인 경우 ''H'' ≤ ''G''임을 보여준다(실제로 모든 ''n''에 대해 성립하는 성질). 또한

G = \sqrt{AH}

이므로, 두 수의 기하 평균은 그 산술 평균과 조화 평균의 기하 평균과 같다.

이 관계는 n(데이터 집합의 크기)이 3 이상인 경우로 확장할 수 있으며, 일반적인 경우의 관계는 다음과 같다:

:

H(x_1, \cdots , x_n)= \frac{(G(x_1, \cdots , x_n))^n}{A(x_2x_3 \cdots x_n, x_1x_3 \cdots x_n, \cdots , x_1x_2 \cdots x_{n-1})}= \frac{(G(x_1, \cdots , x_n))^n}{A\left( \frac{\prod_{i=1}^n x_i}{x_1}, \frac{\prod_{i=1}^n x_i}{x_2},\cdots , \frac{\prod_{i=1}^n x_i}{x_n} \right)}.

이 관계식은 조화 평균의 정의식을 변형한 식

:

H = \frac{n}{\sum\limits_{i=1}^n \frac{1}{x_i}}= \frac{n \prod\limits_{j=1}^n x_j }{ \sum\limits_{i=1}^n \frac{\prod_{j=1}^n x_j}{x_i}}

에서 유도된다.

세 수의 평균에서는 다음 관계가 성립한다^[37]：

:

\frac{A^3}{G^3}+\frac{G^3}{H^3}+1 \leq \frac{3}{4} \left(1+\frac{A}{H} \right)^2

5. 응용

어떤 경우에는 조화 평균이 정확한 평균값을 제공한다. 예를 들어, 전체 거리의 절반을 40km/h의 속력으로 이동하고, 나머지 절반을 60km/h의 속력으로 이동했다면, 평균 속력은 40과 60의 조화 평균인 48km/h가 된다. 이는 이동하는 데 전체 거리를 48km/h의 속력으로 달린 경우와 같은 시간이 걸렸기 때문이다. (만약 전체 "시간"의 절반씩을 달렸다면, 평균 속력은 산술 평균인 50km/h가 된다.)

5. 1. 물리학

어떤 차량이 속도 ''x''(예: 60km প্রতি ঘণ্টা)로 특정 거리 ''d''를 이동하고 속도 ''y''(예: 20km প্রতি ঘণ্টা)로 같은 거리를 되돌아온다면, 평균 속도는 ''x''와 ''y''의 조화 평균(30km প্রতি ঘণ্টা)이며 산술 평균(40km প্রতি ঘণ্টা)이 아니다. 총 이동 시간은 그 평균 속도로 전체 거리를 이동한 경우와 동일하다.^[11]

그러나 차량이 속도 ''x''로 특정 시간 ''t'' 동안 이동한 다음 같은 시간 동안 속도 ''y''로 이동하는 경우 평균 속도는 ''x''와 ''y''의 산술 평균이며, 위의 예에서는 40km প্রতি ঘণ্টা이다.

같은 원리가 둘 이상의 구간에도 적용된다. 서로 다른 속도로 여러 개의 하위 여정이 있는 경우, 각 하위 여정이 같은 ''거리''를 이동한다면 평균 속도는 모든 하위 여정 속도의 ''조화'' 평균이며, 각 하위 여정이 같은 ''시간''이 걸린다면 평균 속도는 모든 하위 여정 속도의 ''산술'' 평균이다. (둘 다 아닌 경우 가중 조화 평균 또는 가중 산술 평균이 필요하다. 산술 평균의 경우, 여정 각 부분의 속도는 해당 부분의 지속 시간에 따라 가중치가 지정되고, 조화 평균의 경우 해당 가중치는 거리이다. 두 경우 모두 결과 공식은 총 거리를 총 시간으로 나누는 것으로 축소된다.)

"거리에 따른 가중치"의 경우 조화 평균을 사용하지 않고도 해결할 수 있다. "느림"이라는 개념을 도입하여 "느림"(시간/킬로미터)이 속도의 역수로 정의한다. 여정의 "느림"을 구한 후 역수를 취하여 "실제" 평균 여정 속도를 구한다. 각 여정 구간 i에 대해 느림 s_i = 1/speed_i이다. 그런 다음 각 거리에 따라 가중치가 지정된 s_i의 산술 평균을 취한다(선택적으로 여정 길이로 나누어 가중치를 정규화하여 합이 1이 되도록 한다). 이렇게 하면 실제 평균 느림(시간/킬로미터)이 구해진다. 이 절차는 조화 평균에 대한 지식 없이도 수행할 수 있으며, 조화 평균을 사용하여 이 문제를 해결할 때 사용하는 것과 같은 수학적 연산과 같다. 따라서 이 경우 조화 평균이 작동하는 이유를 보여준다.

마찬가지로, 구성 원소의 밀도와 질량 분율(또는 동등하게 질량 백분율)을 고려하여 합금의 밀도를 추정하려는 경우, 원자 충진 효과로 인한 일반적으로 미미한 부피 변화를 제외하고 합금의 예상 밀도는 처음 예상할 수 있는 것처럼 가중 산술 평균이 아니라 질량으로 가중된 개별 밀도의 가중 조화 평균이다. 가중 산술 평균을 사용하려면 밀도를 부피로 가중해야 한다. 원소별로 질량 단위에 레이블을 지정하고 같은 원소 질량만 상쇄되도록 하면서 문제에 차원 분석을 적용하면 이것이 명확해진다.

두 개의 전기 저항을 병렬로 연결하면, 하나의 저항이 ''x'' (예: 60 Ω)이고 다른 하나의 저항이 ''y'' (예: 40 Ω)일 때, 그 효과는 ''x''와 ''y''의 조화 평균(48 Ω)과 같은 저항을 가진 두 개의 저항을 사용한 것과 같다. 어느 경우든 등가 저항은 24 Ω(조화 평균의 절반)이다. 이러한 원리는 축전기 직렬 연결 또는 인덕터 병렬 연결에도 적용된다.

그러나 저항을 직렬로 연결하면 평균 저항은 ''x''와 ''y''의 산술 평균(50 Ω)이 되고, 총 저항은 이의 두 배인 ''x''와 ''y''의 합(100 Ω)이 된다. 이 원리는 축전기 병렬 연결 또는 인덕터 직렬 연결에도 적용된다.

앞의 예와 마찬가지로, 두 개 이상의 저항, 축전기 또는 인덕터를 연결할 때도, 모두 병렬로 연결되거나 모두 직렬로 연결되는 경우 동일한 원리가 적용된다.

반도체의 "전도도 유효 질량" 또한 세 가지 결정학적 방향을 따라 유효 질량의 조화 평균으로 정의된다.^[12]

다른 광학 방정식과 마찬가지로, 얇은 렌즈 방정식은 초점거리 ''f''가 렌즈로부터 피사체 ''u''와 상 ''v''의 거리의 조화 평균의 절반임을 나타내도록 다시 쓸 수 있다.^[13]

초점거리 ''f''₁과 ''f''₂인 두 개의 얇은 렌즈가 직렬로 연결된 것은 초점거리가 그들의 조화 평균인 두 개의 얇은 렌즈가 직렬로 연결된 것과 같다. 광학 파워로 표현하면, 광학 파워 ''P''₁과 ''P''₂인 두 개의 얇은 렌즈가 직렬로 연결된 것은 광학 파워가 그들의 산술 평균인 두 개의 얇은 렌즈가 직렬로 연결된 것과 같다.

5. 2. 금융

주가수익비율(P/E)과 같이 여러 배수를 평균낼 때는 가중 조화 평균이 더 적절하다. 이러한 비율들을 가중 산술 평균으로 평균내면, 높은 데이터 지점이 낮은 데이터 지점보다 더 큰 가중치를 받게 된다. 반면에 가중 조화 평균은 각 데이터 지점에 올바르게 가중치를 부여한다.^[14] 가격으로 정규화되지 않은 비율에 단순 가중 산술 평균을 적용하면 상향 편향되며, 동일한 수익을 기반으로 하기 때문에 수치적으로 정당화될 수 없다. 이는 마치 왕복 여정의 차량 속도를 평균낼 수 없는 것과 같다.^[15]

5. 3. 기하학

두 수 ''x''와 ''y''의 조화 평균 ''z''의 그래픽 해석과 이를 계산하기 위한 노모그램. 파란색 선은 6과 2의 조화 평균이 3임을 보여줍니다. 마젠타색 선은 6과 −2의 조화 평균이 −6임을 보여줍니다. 빨간색 선은 어떤 수와 그 수의 음수의 조화 평균이 선이 ''z''축과 교차하지 않으므로 정의되지 않음을 보여줍니다.

엇갈린 사다리. ''h''는 ''A''와 ''B''의 조화 평균의 절반이다.

임의의 삼각형에서 내접원의 반지름은 높이의 조화 평균의 1/3이다.
정삼각형 ABC의 외접원의 작은 호 BC 위의 임의의 점 P에 대해, B와 C로부터의 거리를 각각 ''q''와 ''t''라고 하고, PA와 BC의 교점이 점 P로부터 ''y''만큼 떨어져 있다면, ''y''는 ''q''와 ''t''의 조화 평균의 절반이다.^[16]
다리의 길이가 ''a''와 ''b''이고, 빗변에서 직각으로 그은 높이가 ''h''인 직각삼각형에서, 는 와 의 조화 평균의 절반이다.^[17]^[18]
빗변이 ''c''인 직각삼각형에 내접하는 두 정사각형의 변을 ''t''와 ''s''(''t'' > ''s'')라고 하자. 그러면 는 와 의 조화 평균의 절반과 같다.
사다리꼴의 꼭짓점을 순서대로 A, B, C, D라고 하고, 평행한 변을 AB와 CD라고 하자. 대각선의 교점을 E라고 하고, FEG가 AB와 CD에 평행하도록 변 DA 위에 F, 변 BC 위에 G를 잡으면, FG는 AB와 DC의 조화 평균이다. (이는 닮은 삼각형을 이용하여 증명할 수 있다.)
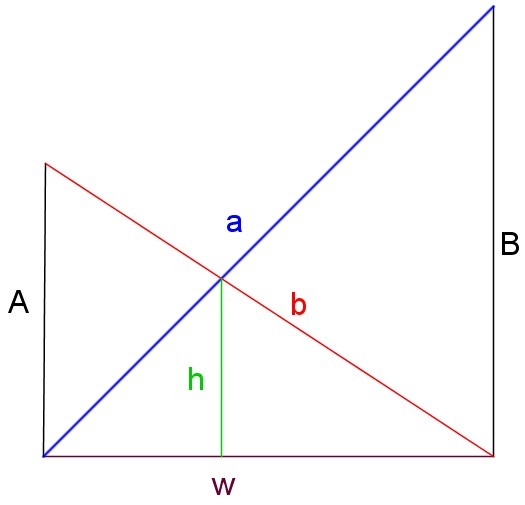
이 사다리꼴 결과의 한 가지 응용은 엇갈린 사다리 문제로, 두 개의 사다리가 골목길 반대편에 놓여 있으며, 각각의 발은 한쪽 벽의 바닥에 있고, 하나는 높이 ''A''의 벽에 기대어 있고, 다른 하나는 반대편 벽에 높이 ''B''로 기대어 있는 경우이다. 그림과 같이 사다리는 골목길 바닥에서 ''h''의 높이에서 교차한다. 그러면 ''h''는 ''A''와 ''B''의 조화 평균의 절반이다. 벽이 기울어져 있지만 여전히 평행하고 "높이" ''A'', ''B'', ''h''가 벽에 평행한 선을 따라 바닥으로부터의 거리로 측정되는 경우에도 이 결과는 여전히 유지된다. 이것은 사다리꼴의 면적 공식과 면적 가산 공식을 사용하여 쉽게 증명할 수 있다.
타원에서 준선(초점에서 단축에 평행한 선을 따라 타원까지의 거리)은 초점으로부터 타원까지의 최대 거리와 최소 거리의 조화 평균이다.

5. 4. 정보 과학

정보학 분야에서는 주로 정보 검색 및 기계 학습에 사용되는 알고리즘이나 시스템을 평가할 때 정밀도와 재현율의 조화 평균인 F-측정값이 사용된다.

5. 5. 기타

수문학에서는 지층이나 토양에 대해 평행한 흐름에 대한 투수계수의 평균을 고려할 때 산술 평균을 사용하는 반면, 수직한 흐름에 대한 투수계수의 평균을 고려할 때 조화 평균이 사용된다. 이러한 차이는 수문학에서 전도도가 저항의 역수이기 때문에 발생한다.^[42]
세이버메트릭스에서는 선수의 지표로서, 홈런 수와 도루 수의 조화 평균인 파워-스피드 넘버(Power–speed number)가 사용된다.
집단 유전학에서는 세대의 개체 수에 급격한 변동이 있었을 때 Effective population size|유효개체수^영어에 미치는 영향을 계산할 때 조화 평균이 사용된다. 이는 매우 개체 수가 적은 세대가 실질적으로 병목 현상이 되어, 매우 적은 수의 개체가 유전자 풀에 불균형적으로 영향을 미치고, 결과적으로 강한 근친 교배가 일어날 수 있다는 점을 고려하기 위해서이다.
교통에서는 속도를 다루기 때문에, 물리학의 경우와 마찬가지로 조화 평균이나 가중 조화 평균을 사용한다.
미국에서 자동차의 연비를 나타낼 때 주로 사용되는 두 단위 '마일/갤런' 및 '리터/100km'의 차원은 서로 역수 관계에 있다(전자는 단위 부피당 거리이고, 후자는 단위 거리당 부피이므로). 따라서, 광범위한 자동차 연비의 평균값을 조사할 때, 한쪽 단위로 산술 평균을 취하면, 그것은 다른 쪽 단위의 조화 평균의 관계가 된다. 예를 들어, 리터/100km 단위로 표시된 연비의 산술 평균값을 마일/갤런으로 변환하면, 마일/갤런 단위로 표시된 연비는 조화 평균값이 된다.
금융에서 조화 평균은 주가수익률과 같은 비율의 평균을 얻는 데 적합한 방법이다.^[42] 만약 이러한 비율을 산술 평균하면(흔한 실수), 큰 값이 작은 값보다 더 가중치가 부여된다. 반면 조화 평균에서는 각 값에 동일한 가중치가 부여된다.
화학과 핵물리학에서 서로 다른 종(예: 분자 또는 동위원소)으로 구성된 혼합물의 입자당 평균 질량은 각 종의 질량을 해당 질량 분율로 가중한 개별 종의 질량의 조화 평균으로 주어진다.

> Effective population size|유효개체수^영어 템플릿 수정.

기타 다른 부분들은 모두 정상적으로 출력됨.

6. 통계

표본 조화 평균의 통계적 성질, 분산 추정 방법, 편향 및 분산 추정량 등이 연구되었다.^[23]

임의 표본에 대해 조화 평균은 기댓값과 분산이 모두 무한대가 될 수 있다(1/0 형태의 항을 하나라도 포함하는 경우). 표본 평균 ''m''은 점근적으로 분산 ''s''²을 갖는 정규분포를 따르며, 평균 자체의 분산은 다음과 같이 나타낼 수 있다.

: $\operatorname{Var}\left(\frac{1}{x}\right) = \frac{m \left[\operatorname{E}\left(\frac{1}{x} - 1\right)\right]}{n m^2}$

여기서 ''m''은 역수들의 산술 평균, ''x''는 변량, ''n''은 모집단 크기, ''E''는 기댓값 연산자이다.

표본에 대한 분산이 무한대가 아니고 중심 극한 정리가 적용된다고 가정하면, 델타 방법을 사용하여 분산은 다음과 같이 나타낼 수 있다.

: $\operatorname{Var}(H) = \frac{1}{n}\frac{s^2}{m^4}$

여기서 ''H''는 조화 평균, ''m''은 역수들의 산술 평균, ''s''²는 자료의 역수들의 분산, ''n''은 표본에 있는 자료점의 개수이다.

조화 평균의 분산을 추정하는 데에는 잭나이프 방법을 사용할 수 있다.^[24] 이 방법은 먼저 표본의 평균(''m'')을 계산하고, 일련의 값 ''w''_i를 계산한 후, ''w''_i의 평균(''h'')을 구하는 방식으로 진행된다. 평균의 분산은 다음과 같이 계산된다.

: $\frac{n - 1}{n} \sum{(m - w_i)}^2.$

이후 t 검정을 사용하여 평균에 대한 유의성 검정과 신뢰 구간을 추정할 수 있다.

크기 편향 표본 추출(Size biased sampling)에서 확률 변수가 분포 ''f''(''x'')를 따르고, 변수가 선택될 가능성이 그 값에 비례한다고 가정하면, 길이 기반 또는 크기 편향 표본 추출이라고 한다. 모집단의 평균을 ''μ''라고 할 때, 크기 편향 모집단의 확률 밀도 함수 ''f''*(''x'')는 다음과 같다.

: $f^*(x) = \frac{x f(x)}{\mu}$

이 길이 편향 분포의 기댓값 E^*(''x'')는 다음과 같다.

: $\operatorname{E}^*(x) = \mu \left[ 1 + \frac{\sigma^2}{\mu^2} \right]$

여기서 ''σ''²는 분산이다. 조화 평균의 기댓값은 길이 편향이 없는 버전 E(''x'')와 같다.

: $E^*( x^{ -1 } ) = E( x )^{ -1 }$

길이 편향 표본 추출 문제는 섬유 제조,^[25] 계보 분석,^[26] 생존 분석^[27] 등 여러 분야에서 발생한다. Akman 등은 표본에서 길이 기반 편향을 검출하기 위한 검정을 개발했다.^[28]

옌센 부등식에 따르면, ''X''와 E(X)가 0보다 크다고 가정하면 다음이 성립한다.

: $\operatorname{E}\left[ \frac{1}{X} \right] \ge \frac{1}{ \operatorname{E}(X) }$

Gurland는^[30] 양의 값만 취하는 분포에 대해, 임의의 n > 0에 대해 다음을 보였다.

: $\operatorname{E} \left(X^{-1}\right) \ge \frac{\operatorname{E} \left(X^{n-1}\right)}{\operatorname{E}\left(X^n\right)} .$

어떤 조건하에서는^[31]

: $\operatorname{E}(a + X)^{-n} \sim \operatorname{E}\left(a + X^{-n}\right)$

여기서 ~는 근사적으로 같음을 의미한다.

변량이 로그정규분포에서 추출되었다고 가정하면, H를 추정하는 여러 가지 방법이 있으며, 그 중 H₃는 25개 이상의 표본에 대해 가장 좋은 추정량일 가능성이 높다.^[32] 수치 실험에서 H₃는 일반적으로 H₁보다 조화 평균의 더 우수한 추정량이며,^[33] H₂는 H₁과 매우 유사한 추정값을 생성한다.

7. 베타 분포, 로그정규분포, 파레토 분포

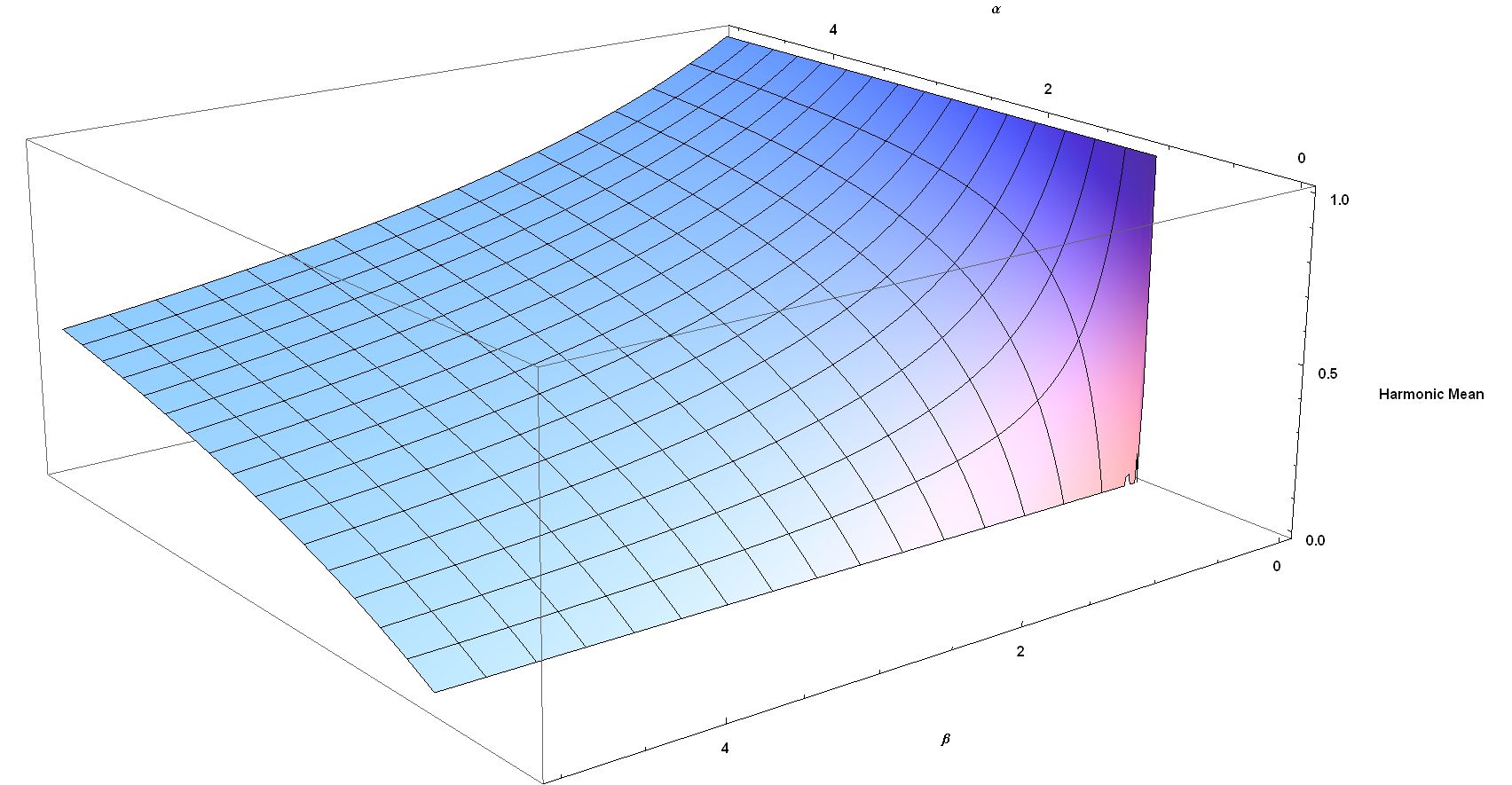
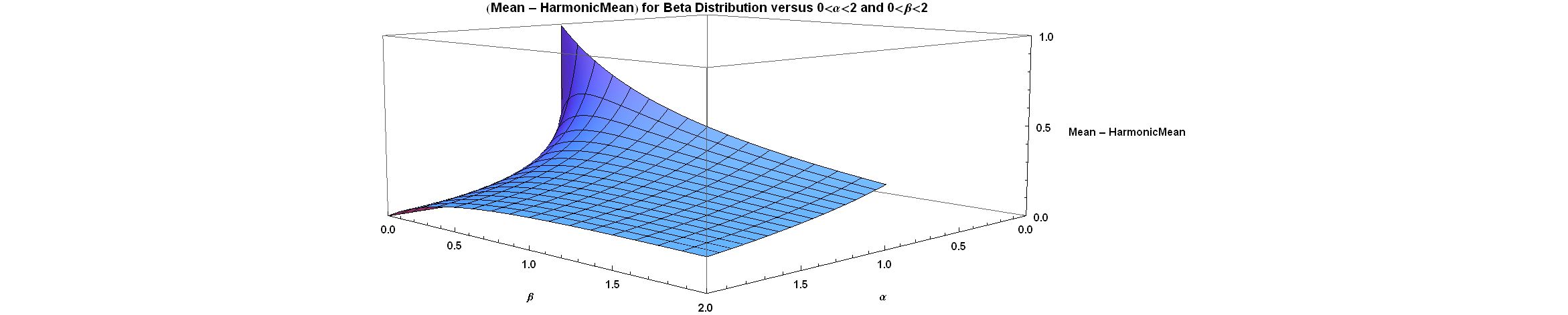
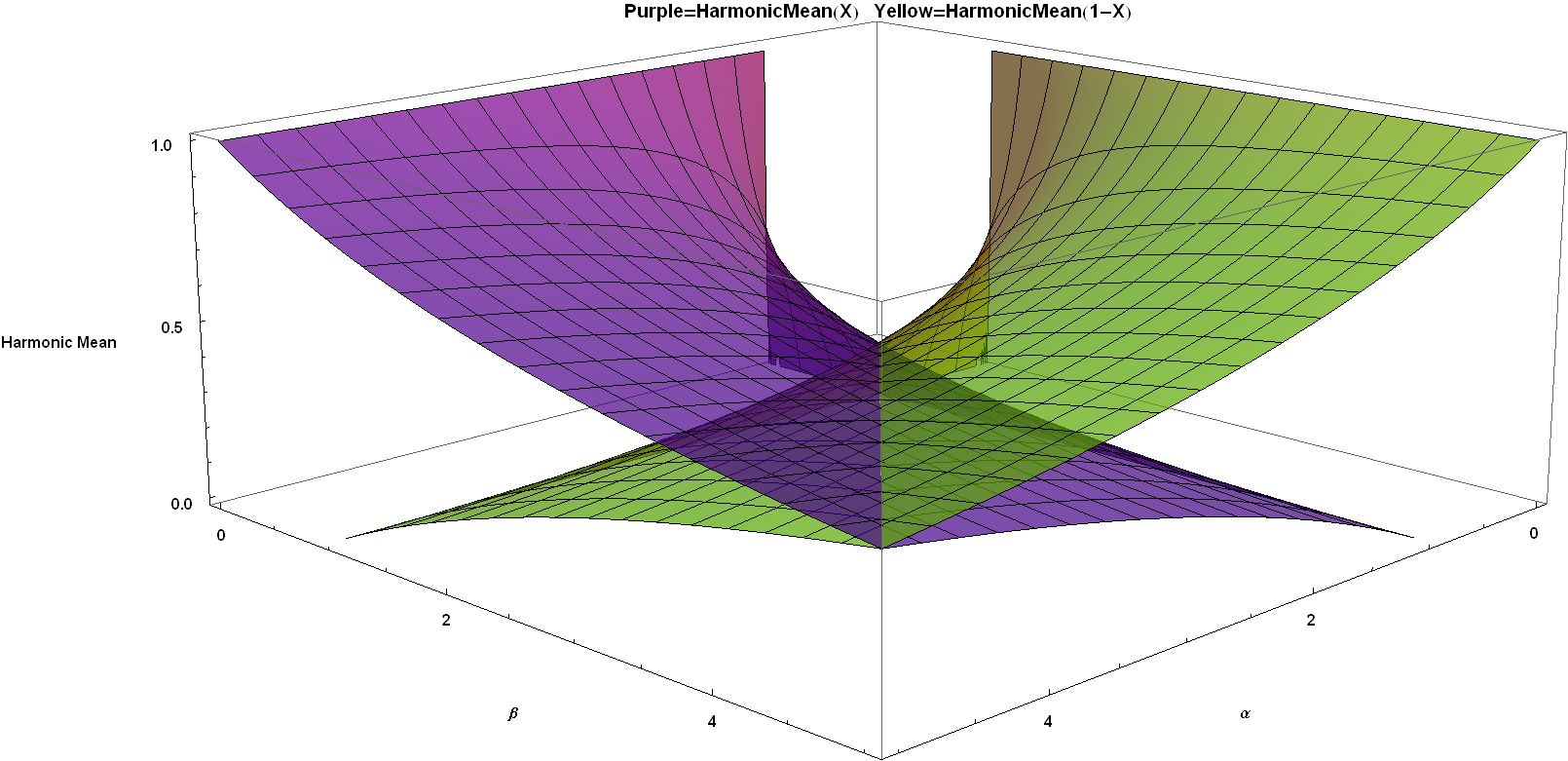
모양 매개변수 ''α''와 ''β''를 갖는 베타 분포의 조화 평균은 다음과 같다.

:

H = \frac{\alpha - 1}{\alpha + \beta - 1} \text{ 단, } \alpha > 1 \, \, \& \, \, \beta > 0

''α'' < 1일 때 조화 평균은 정의되지 않는데, 이는 정의식이 [0, 1]에서 경계가 없기 때문이다.

''α'' = ''β''일 때,

:

H = \frac{\alpha - 1}{2 \alpha - 1}

이는 조화 평균이 ''α'' = ''β'' = 1일 때 0에서 ''α'' = ''β'' → ∞일 때 1/2까지의 범위를 갖는다는 것을 보여준다.

다음은 하나의 매개변수가 유한(0이 아님)하고 다른 매개변수가 이러한 한계에 접근할 때의 한계이다.

:

\begin{align}\lim_{\alpha \to 0} H &= \text{ 정의되지 않음 } \\\lim_{\alpha \to 1} H &= \lim_{\beta \to \infty}  H = 0 \\\lim_{\beta \to 0}  H &= \lim_{\alpha \to \infty} H = 1\end{align}

기하 평균과 마찬가지로 조화 평균은 네 매개변수 케이스의 최대 가능도 추정에 유용할 수 있다.

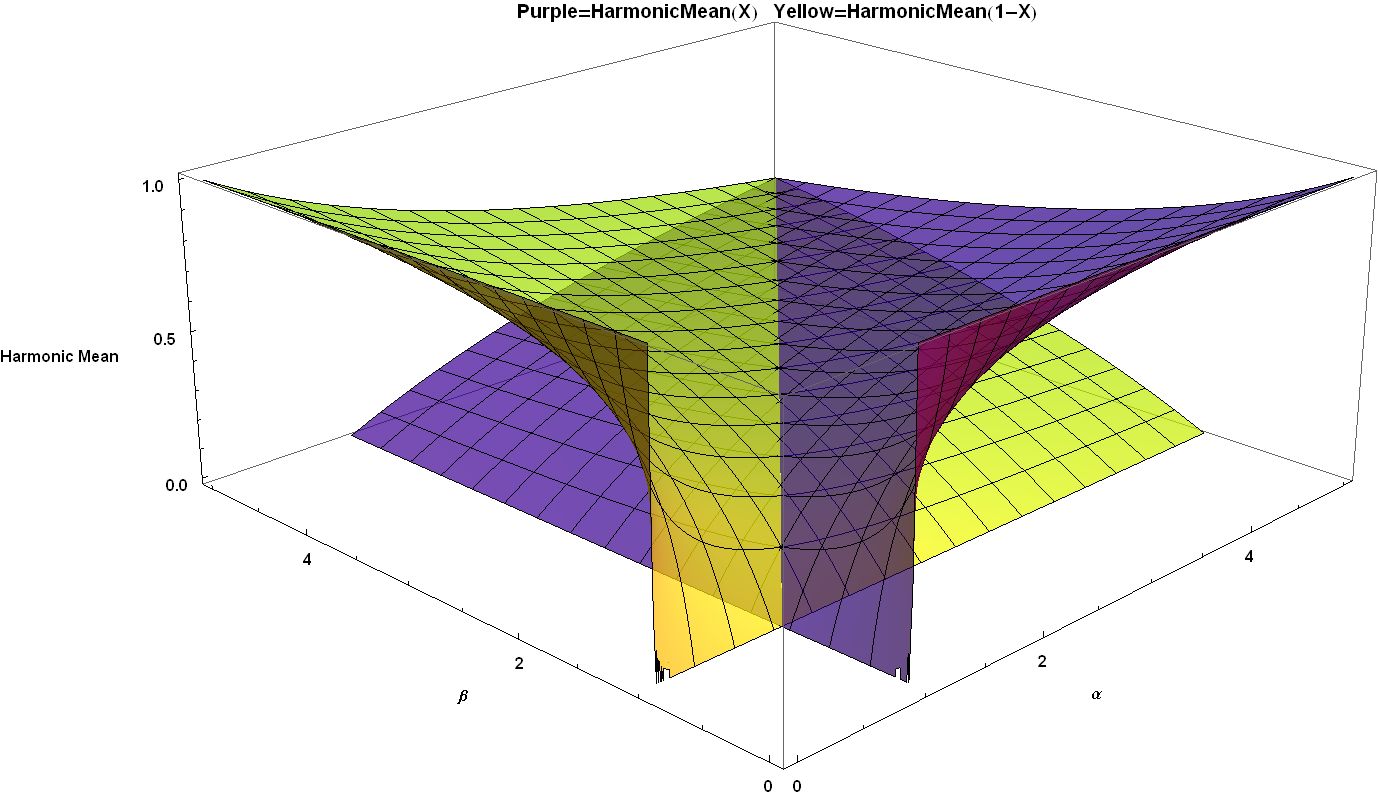
이 분포에는 두 번째 조화 평균 (''H''_{1 − X})도 존재한다.

:

H_{1-X} =  \frac{\beta - 1}{\alpha + \beta - 1} \text{ 단, } \beta > 1 \, \, \& \, \, \alpha > 0

''β'' < 1일 때 이 조화 평균은 정의되지 않는데, 이는 정의식이 [0, 1]에서 경계가 없기 때문이다.

''α'' = ''β''일 때,

:

H_{1-X} = \frac{\beta - 1}{2 \beta - 1}

이는 조화 평균이 ''α'' = ''β'' = 1일 때 0에서 ''α'' = ''β'' → ∞일 때 1/2까지의 범위를 갖는다는 것을 보여준다.

다음은 하나의 매개변수가 유한(0이 아님)하고 다른 매개변수가 이러한 한계에 접근할 때의 한계이다.

:

\begin{align}\lim_{\beta \to 0}  H_{1-X} &= \text{ 정의되지 않음 } \\\lim_{\beta \to 1}  H_{1-X} &= \lim_{\alpha \to \infty} H_{1-X} = 0 \\\lim_{\alpha \to 0} H_{1-X} &= \lim_{\beta \to \infty}  H_{1-X} = 1\end{align}

두 조화 평균 모두 비대칭이지만, ''α'' = ''β''일 때 두 평균은 같다.

확률변수 X에 대한 로그정규분포의 조화평균(H)은 다음과 같다.^[20]

:

H = \exp \left( \mu - \frac{1}{2} \sigma^2 \right),

여기서 μ와 σ²은 분포의 모수, 즉 X의 자연로그 분포의 평균과 분산이다.

분포의 조화평균과 산술평균은 다음과 같은 관계가 있다.

:

\frac{\mu^*}{H} = 1 + C_v^2 \, ,

여기서 C_v와 μ^*는 각각 분포의 변동계수와 평균이다.

분포의 기하평균(G), 산술평균, 조화평균은 다음과 같은 관계가 있다.^[21]

:

H \mu^* = G^2.

제1종 파레토 분포의 조화 평균은^[22]

:

H = k \left( 1 + \frac{1}{\alpha} \right)

여기서 ''k''는 척도 매개변수이고 ''α''는 형상 매개변수이다.

참조

_[1] 웹아카이브 Course https://www.comap.co[...] 2022-07-11
_[2] 서적 Quantitative Techniques for Managerial Decisions https://books.google[...] New Age International 1989
_[3] 서적 Probability, Statistics and Other Frightening Stuff https://books.google[...] Routledge 2018-10-09
_[4] 웹사이트 Harmonic Mean https://mathworld.wo[...] 2023-05-31
_[5] 논문 A proof of the arithmetic mean-geometric mean-harmonic mean inequalities http://ajmaa.org/RGM[...] 2015-12-22
_[6] 서적 Statistical Analysis Holt International 1969
_[7] 간행물 More on spreads and non-arithmetic means 2004-03
_[8] 웹사이트 Archived copy http://www.imomath.c[...] 2014-10-15
_[9] 간행물 The nature and use of the harmonic mean 1931
_[10] arXiv On a Double Series Representation of the Natural Logarithm, the Asymptotic Behavior of Hölder Means, and an Elementary Estimate for the Prime Counting Function
_[11] 웹사이트 Average: How to calculate Average, Formula, Weighted average https://learningpund[...] 2018-05-08
_[12] 웹사이트 Effective mass in semiconductors http://ecee.colorado[...] 2018-05-08
_[13] 서적 Optics Addison Wesley
_[14] 서적 The Handbook of Business Valuation and Intellectual Property Analysis McGraw Hill
_[15] 학술지 Using the Price-to-Earnings Harmonic Mean to Improve Firm Valuation Estimates
_[16] 서적 Challenging Problems in Geometry https://archive.org/[...] Dover
_[17] 간행물 Integer solutions of $a^{-2}+b^{-2}=d^{-2}$ 1999-07
_[18] 간행물 The upside-down Pythagorean Theorem 2008-07
_[19] 서적 Information Retrieval http://www.dcs.gla.a[...] Butterworth
_[20] 서적 The lognormal distribution with special reference to its uses in economics Cambridge University Press
_[21] 간행물 Design stream flows based on harmonic means
_[22] 서적 Continuous univariate distributions Vol 1
_[23] 간행물 Length-biased sampling and biomedical problems Biometric Society Meeting
_[24] 간행물 Estimate of variance for harmonic mean half lives
_[25] 간행물 Some sampling problems in technology Wiley Interscience
_[26] 간행물 Referent sampling, family history and relative risk: the role of length-biased sampling
_[27] 간행물 On the theory of screening for chronic diseases
_[28] 간행물 A simple test for detection of length-biased sampling
_[29] 간행물 Convex functions of random variables
_[30] 간행물 An inequality satisfied by the expectation of the reciprocal of a random variable
_[31] 간행물 On inverse moments for a class of nonnegative random variables
_[32] 간행물 Fitting lognormal distributions to hydrologic data
_[33] 간행물 Estimation of harmonic mean of a lognormal variable http://engineering.t[...]
_[34] 간행물 Technical support document for water quality-based toxics control Office of Water
_[35] 서적 The flow of homogeneous fluids through porous media McGraw-Hill
_[36] 서적 Statistical Analysis Holt International
_[37] 웹사이트 Inequalities proposed in “Crux Mathematicorum” http://www.imomath.c[...]
_[38] 간행물 More on spreads and non-arithmetic means 2004-03
_[39] 서적 Challenging Problems in Geometry Dover Publ. Co.
_[40] 간행물 Integer solutions of {{math|1=''a''{{sup|−2}} + ''b''{{sup|−2}} = ''d''{{sup|−2}}}} 1999-07
_[41] 간행물 The upside-down Pythagorean Theorem 2008-07
_[42] 서적 Fairness Opinions: Common Errors and Omissions McGraw Hill

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com